Real Analysis Notes

Table of Contents:

Uniform Convergence

Outline:

Intro and Motivation
Pointwise and Uniform convergence
Weistrass M Test
Integration and Differentiation of Series
The Elementary Functions
The Space of Continuous Functions
The Arzela-Ascoli Theorem
The Contraction Mapping Principle and Its Applications
The Stone-Weistrass Theorem
The Dirichlet and Abel Tests
Power Series and Cesaro and Abel Summability
Examples and Exercises (end of chapter).
intro:
- many important functions are defined using infinite sequences or infinite series. We need specific tests to study the uniform convergence of such functions.
- Some helpful tests are : Weistrass M Test for series and the Cauchy criterion, everything else is more specialized.
- for uniform convergence we deal with the vector space of continuous functions.
  - here the “vectors” or “points” are continuous functions.
  - here the convergence of a sequence \( == \) uniform convergence of these continuous functions.
  - This space is complete (why?) because Cauchy sequences converge within it.
  - Thus space has the Arzela-Ascoli theorem applied in it, which talks about compactness of some subsets.
  - The Stone Weistrass Theorem is also useful here, it allows you to approximate continuous functoins by series.
  - The contraction mapping principle leads the way to applications to integration and differentiation.
Pointwise and Uniform Convergence:
- pointwise is the most natural way to think about convergence.
  - (why?) because we only ask for each point \(x\) in the domain the sequence \(f_{k}(x)\) converges.
- pointwise convergence (def) :
  - \(N\) is a metric space. A is a set. \(f_{k} : A \mapsto N\) for \(k = 1,2,3…..\)
  - then the sequence of functions \(f_{k}\) is said to converge pointwise/ converge simply to a function \(f : A \mapsto N\) if…
    - for each \(x \in A\),
    - \(f_{k}(x) \mapsto f(x)\) (convergences to f(x) as a sequence in the metric space N) (QUESTION: revisit convergence in metric spaces)
  - so the “point” f is the point of convergence of the sequence of “points” \(f_{k}(x)\).
  - When does pointwise conv not help?
    - f, the function the sequence converges to, does not need to be contunuous, even if the \(f_{k}\) are cont.
      - ex: consider this function:
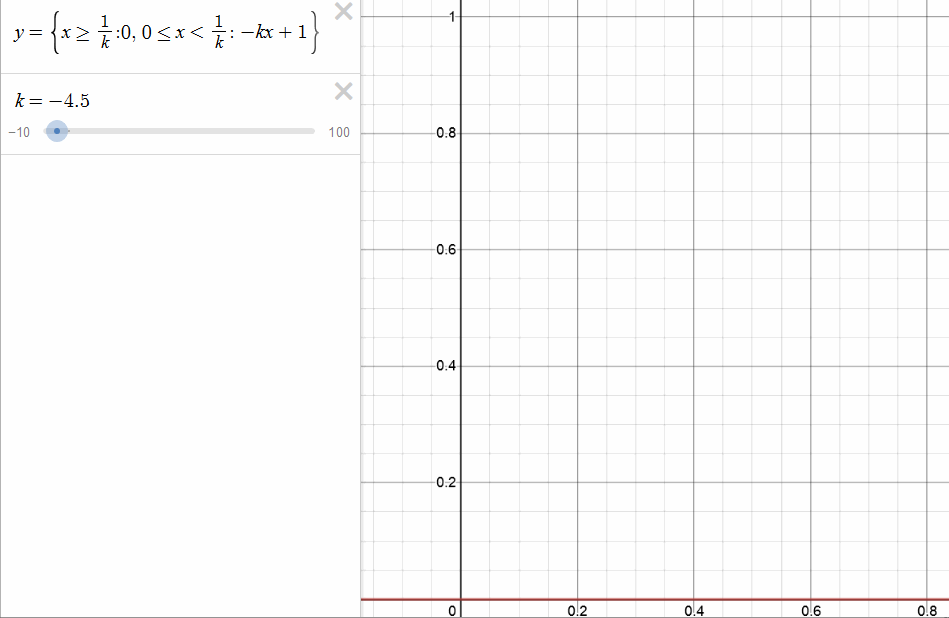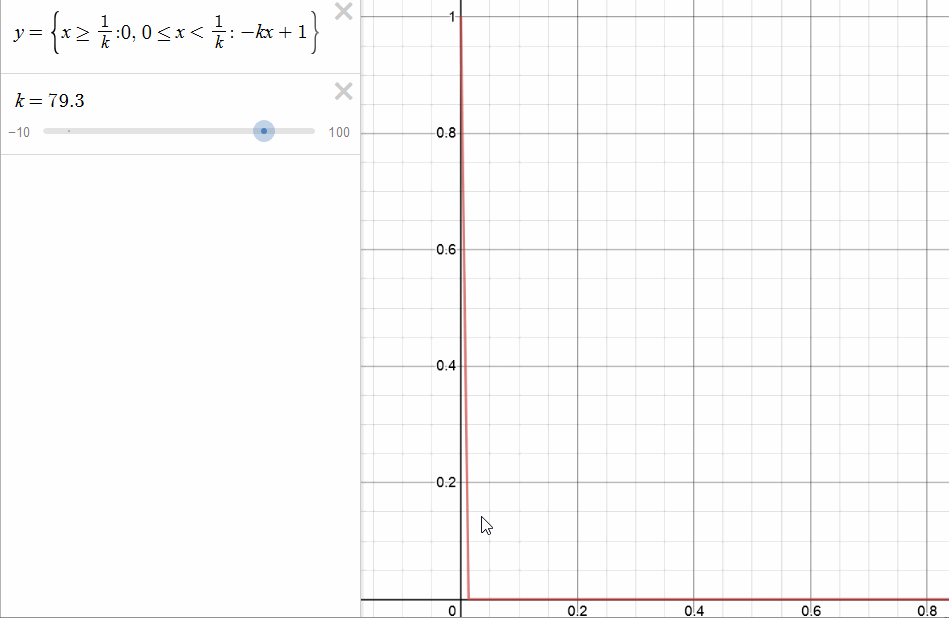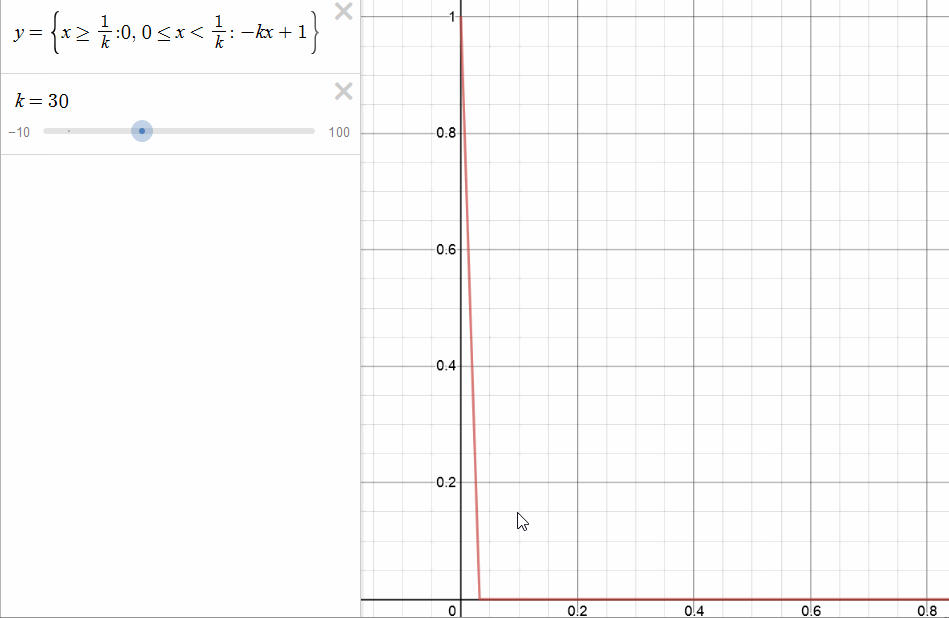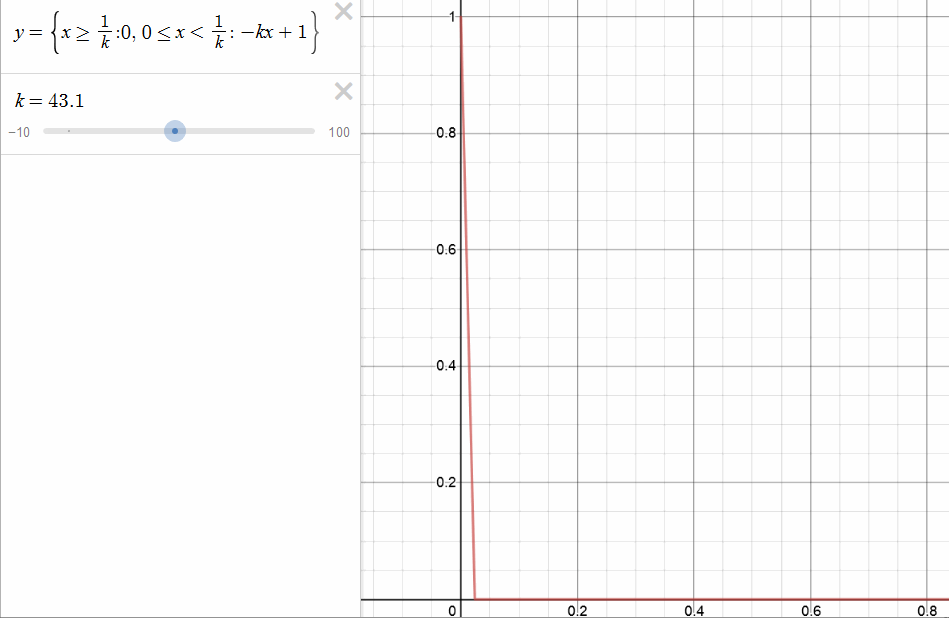
      - so the limit function is defined as \(f(x)\) = \( \begin{cases} 1 & x=0 \
        0 & x > 0 \end{cases} \), but this is discontinuous, even though each \(f_{k}(x)\) is continuous. Here convergence relies on choice of x, we need bigger k for smaller x.
      - We ask then for uniformity of closeness, regardless of the x value.
EXERCISE (5.1) (a): if \(f_{k} \mapsto f\) (pointwise) and \(g_{k} \mapsto g\) (pointwise), then prove that \(f_{k} + g_{k} \mapsto f + g\)(pointwise) for functions \(f,g \in \)
uniformly continuous